How do I figure out this compound miter setting?
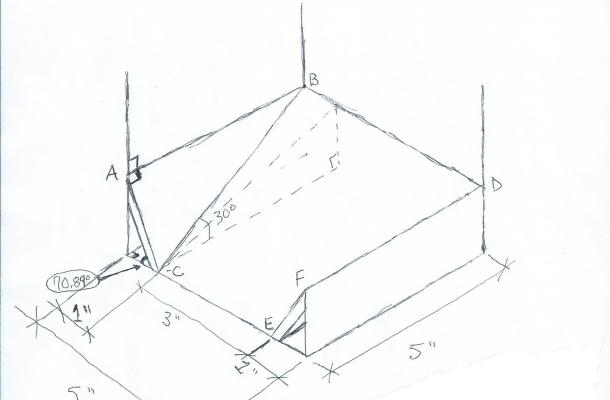
I was designing a dice tower and settled for a less complicated design on this one because I couldn't wrap my head around this one. Essentially, it's a box with internal dimensions of 5"x5"x13.75", with a number of angled planes partially blocking the column. At the bottom was to be a 3-sided ramp leading out of an opening in one of the sides of the box.
That ramp (and some other pieces I abandoned) has me absolutely stumped. The main portion of the ramp was to be a trapezoidal figure of 3" wide at the bottom front of the box, 5" wide at the back of the box, spanning the depth of the box (5") at an inclination of 30 degrees. The side pieces of the ramp would come from the back of the box to the front of the box, at a level height equal to the back of the main ramp, and would meet the main ramp figure in a compound miter. That compound miter is turning my brain to mush.
While I would really like to have the specific miter and bevel angles necessary to make these cuts, just for the sake of closure, I would appreciate even more an explanation of how to figure these sorts of problems out. I'm not exactly a chump when it comes to math, but I simply couldn't wrap my head around this one. Manipulation of trig functions in 3D space, when dealing with possibly four intersecting planes, becomes a bit hard to figure out without any outside help.
Thanks for your time and consideration! Attached is a sketch showing what was intended.